Bitcoin Ecdsa Key Openssl Generate Address

In your generateaddressfrompublickeyhash method, the checksum should be over the hash including the address prefix. You’re not actually using the pk variable at. Mar 20, 2020  Python Bitcoin Library. Bitcoin, Litecoin and Dash Crypto Currency Library for Python. Includes a fully functional wallet, with multi signature, multi currency and multiple accounts. You this library at a high level and create and manage wallets for the command line or at a low level and create your own custom made transactions, keys or wallets.

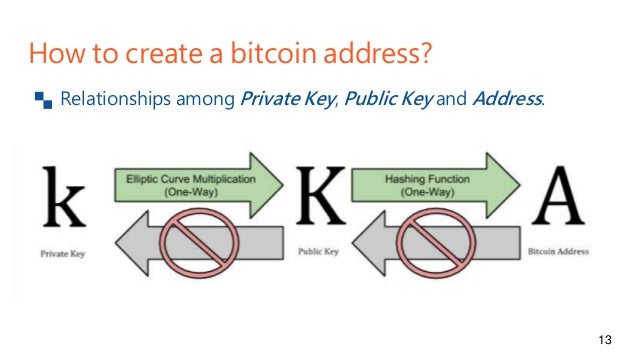
Elliptic Curve Digital Signature Algorithm or ECDSA is a cryptographic algorithm used by Bitcoin to ensure that funds can only be spent by their rightful owners.

A few concepts related to ECDSA:

• private key: A secret number, known only to the person that generated it. A private key is essentially a randomly generated number. In Bitcoin, someone with the private key that corresponds to funds on the block chain can spend the funds. In Bitcoin, a private key is a single unsigned 256 bit integer (32 bytes).
• public key: A number that corresponds to a private key, but does not need to be kept secret. A public key can be calculated from a private key, but not vice versa. A public key can be used to determine if a signature is genuine (in other words, produced with the proper key) without requiring the private key to be divulged. In Bitcoin, public keys are either compressed or uncompressed. Compressed public keys are 33 bytes, consisting of a prefix either 0x02 or 0x03, and a 256-bit integer called x. The older uncompressed keys are 65 bytes, consisting of constant prefix (0x04), followed by two 256-bit integers called x and y (2 * 32 bytes). The prefix of a compressed key allows for the y value to be derived from the x value.
• signature: A number that proves that a signing operation took place. A signature is mathematically generated from a hash of something to be signed, plus a private key. The signature itself is two numbers known as r and s. With the public key, a mathematical algorithm can be used on the signature to determine that it was originally produced from the hash and the private key, without needing to know the private key. Resulting signatures are either 73, 72, or 71 bytes long (with approximate probabilities of 25%, 50%, and 25%, respectively--although sizes even smaller than that are possible with exponentially decreasing probability).^[1]

See also

References

There is no limit to how many public addresses a user can generate. In order to generate such a key and subsequently a wallet address, there have to be applied a number of conversions to the private key. These conversions are known as hash functions, which are un-reversible conversions. Creating a Public Key with ECDSA. The public portion of a keypair which can be used to verify signatures made with the private portion of the keypair. An ECDSA public key that is 33 bytes long rather than the 65 bytes of an uncompressed public key. Public key formats — Bitcoin.org Developer Guide. What is a compressed public key? — Bitcoin StackExchange. Why does Bitcoin Core support both compressed and uncompressed keys? — Bitcoin StackExchange. Support Bitcoin.org: Donate. This article will review the mechanism of digital signatures by creating a self-signed CA. Aiming to create a self-certification authority in ECDSA format, which is being adopted in the IoT. Three very small observations: In your function generateprivatekeywif, you never use hashed, you re-compute it for the return value. In a nice self-contained module like this one, you should definitely add docstrings to your functions.Have a look at PEP257 to see how they are defined. You currently do from ecdsa.keys import SigningKey, but never use it.

1. ↑'ECDSA Signature Probability Basis'. https://crypto.stackexchange.com/a/75997/28556/.

External Links

What is a Private Key?

A private key is a secret 256-bit long number randomly selected when you create a Bitcoin wallet. This is the address which enables you to send the Bitcoins to a recipient’s address. You never share the private key to anyone.

The number and type of cryptographic functions implemented for security reasons defines just how random and unique the key is.

A private uncompressed key always begins with a 5 and it looks like this:

5Hwgr3u458GLafKBgxtssHSPqJnYoGrSzgQsPwLFhLNYskDPyyA

What is a Public Key?

A public key is another address consisting of numbers and letters which is a derivate from private keys after they have been encrypted via the use of mathematical functions. The encryption process cannot be reversed and thus no one can find out the original private key. This is the address that enables you to receive Bitcoins.

The hash of a public key is always 1:

1BvBMSEYstWetqTFn5Au4m4GFg7xJaNVN2

This address you publicly make available in order to receive Bitcoins. There is no limit to how many public addresses a user can generate. In order to generate such a key and subsequently a wallet address, there have to be applied a number of conversions to the private key. These conversions are known as hash functions, which are un-reversible conversions.

Creating a Public Key with ECDSA

The first thing you have to do is apply to your private key an ECDSA, also know as Elliptic Curve Digital Signature Algorithm. An elliptic curve is defined by the equation y² = x³ + ax + b with selected value for a and b. There is an entire family of these curves which can be applied. Bitcoin makes use of the secp256k1 curve.

Applying an ECDSA to the private key will result in a 64-byte integer composed of two 32-byte integers put together which represent the X and Y of the point on the elliptic curve.

Below is the code you would require in Python language: Microsoft product key generator 2007.

private_key_bytes = codecs.decode(private_key, ‘hex’)

# Get ECDSA public key

key = ecdsa.SigningKey.from_string(private_key_bytes, curve=ecdsa.SECP256k1).verifying_key

key_bytes = key.to_string()

key_hex = codecs.encode(key_bytes, ‘hex’)

In the code presented above the private keys were decoded with codecs. As in Python, there are at least two classes that can keep the private and public keys, “str”, a string array, and “bytes”- a byte array, things can get a little confusing.

This is because an X string array is not equal to an X byte array, but it equals the byte array with two elements, O<. The codecs.decode method converts a string into a byte array.

After applying ECDSA, we will have to add the bytes 0x04 (04 as a prefix) to the resulted public key. This will generate a Bitcoin full public key.

Compressing the public key

Instead of using the long version of the public key we can compress it to be shorter.

This is done by taking the X from the ECDSA public key and adding 0x02 if the last byte of Y is even, and the 0x03 byte if the last byte is odd.

Encrypting the Key with SHA-256 And RIPEMD-160

Now we move on to create our wallet address. Regardless of the method applied to the public key, the procedure is the same. Obviously, you will have different resulting addresses.

For this, we will need to apply two hash functions: first, we apply SHA-256 to the public key, and then encrypt the result using RIPEMD-160. It is very important that the algorithms are applied in this exact order.

At the end of this process, you will have a 160-bit integer which represents an encrypted public key.

Below is the code needed to encrypt the public key in Python:

public_key_bytes = codecs.decode(public_key, ‘hex’)

# Run SHA-256 for the public key

sha256_bpk = hashlib.sha256(public_key_bytes)

sha256_bpk_digest = sha256_bpk.digest()

# Run RIPEMD-160 for the SHA-256

ripemd160_bpk = hashlib.new(‘ripemd160’)

ripemd160_bpk.update(sha256_bpk_digest)

ripemd160_bpk_digest = ripemd160_bpk.digest()

ripemd160_bpk_hex = codecs.encode(ripemd160_bpk_digest, ‘hex’)

Adding the network byte

As Bitcoin has two networks, main and test, we will need to create an address which will be used on the mainnet. This means that we will have to add 0x00 bytes to the encrypted public key. For testnet use, you would have to add 0x6f bytes.

Calculating the Checksum

The next step is to calculate the checksum of the resulted mainnet key. A checksum ensures that the key has still maintained its integrity during the process. If the checksum does not match, the address will be marked as invalid.

In order to generate a key’s checksum, the SHA-256 hash function must be applied twice and then take the first 4 bytes from this result. Keep in mind that 4 bytes represent 8 hex digits.

The code required for calculating an address checksum is:

# Double SHA256 to get checksum

sha256_nbpk = hashlib.sha256(network_bitcoin_public_key_bytes)

sha256_nbpk_digest = sha256_nbpk.digest()

sha256_2_nbpk = hashlib.sha256(sha256_nbpk_digest)

sha256_2_nbpk_digest = sha256_2_nbpk.digest()

sha256_2_hex = codecs.encode(sha256_2_nbpk_digest, ‘hex’)

checksum = sha256_2_hex[:8]

Now the last step required to make an address is to merge the mainnet key and the checksum.

Encoding the Key with Base58

You will notice that the resulted key does not look like other BTC addresses. This is because most convert them to a Base58 address.

Below is the algorithm needed to convert a hex address to a Base58 address:

def base58(address_hex):

alphabet = ‘123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz’

Bitcoin Ecdsa Key Openssl Generate Address Generator

b58_string = ‘’

# Get the number of leading zeros

leading_zeros = len(address_hex) — len(address_hex.lstrip(‘0’))

# Convert hex to decimal

address_int = int(address_hex, 16)

# Append digits to the start of string

while address_int > 0:

digit = address_int % 58

digit_char = alphabet[digit]

b58_string = digit_char + b58_string

address_int //= 58

# Add ‘1’ for each 2 leading zeros

Openssl Generate Ecc Key

ones = leading_zeros // 2

for one in range(ones):

b58_string = ‘1’ + b58_string

return b58_string

The resulted string will represent a compressed Bitcoin wallet address.

Conclusion

The process of generating a Bitcoin wallet address from a private key is not that difficult if you pay close attention to the aforementioned steps.

If your private key is full or compressed, the resulting addresses will look different, but both of them are just as valid.